Công thức tính góc giữa 2 mặt phẳng và bài tập có lời giải

Bạn đang tìm kiếm một công thức tính góc giữa 2 mặt phẳng? Bạn khó khăn với những định nghĩa về góc giữa 2 mặt phẳng? Đừng lo, bài viết dưới đây chúng ta cùng đi tìm hiểu về định nghĩa, cách xác định, công thức tính góc giữa 2 mặt phẳng, và một số bài tập có lời giải chi tiết để bạn đọc hiểu rõ nhé.

Xem thêm:

• Công thức tính góc giữa hai đường thẳng và bài tập có lời giải
• Công thức tính góc giữa 2 vecto trong không gian và bài tập có lời giải
• Công thức thế năng trọng trường và bài tập có lời giải

Định nghĩa góc giữa 2 mặt phẳng là gì?

Góc giữa 2 mặt phẳng trong không gian là góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Trong không gian 3 chiều, góc giữa hai mặt phẳng còn có tên gọi khác là góc khối. Nó chính là phần không gian bị giới hạn bởi 2 mặt phẳng. Góc giữa 2 mặt phẳng được đo bằng góc giữa 2 đường thẳng nằm trên 2 mặt phẳng có cùng trục giao với giao tuyến của 2 mặt phẳng đó.

Tính chất góc giữa 2 mặt phẳng là:

• Góc giữa 2 mặt phẳng song song và bằng 0^o
• Góc giữa 2 mặt phẳng trùng nhau và bằng 0^o

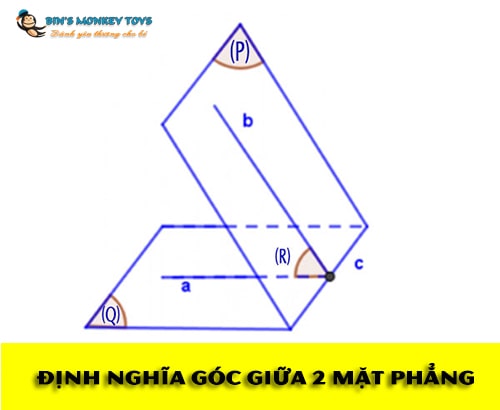
Cách xác định góc giữa hai mặt phẳng

Ví dụ: Gọi P là mặt phẳng 1 và Q là mặt phẳng 2

• Trường hợp 1: 2 mặt phẳng P và Q song song hoặc trùng nhau thì góc của 2 mặt phẳng đó = 0
• Trường hợp 2: 2 mặt phẳng P và Q không song song hoặc trùng với nhau

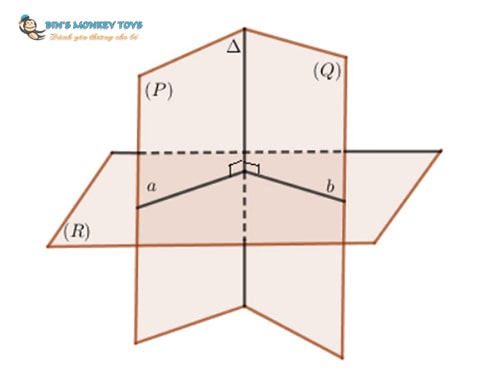
Để xác định góc giữa 2 mặt phẳng bạn áp dụng những cách như sau:

• Cách 1: Dựng 2 mặt phẳng n và p vuông góc với 2 mặt phẳng P và Q. Từ đó góc giữa 2 mặt phẳng P và Q là góc giữa 2 đường thẳng n và p
• Cách 2: Để xác định góc giữa 2 mặt phẳng thì việc đầu tiên bạn cần xác định được giao tuyến ∆ của 2 mặt phẳng P và Q. Sau đó bạn tìm một mặt phẳng R vuông góc với giao tuyến ∆ của 2 mặt phẳng P và Q và cắt 2 mặt phẳng đó tại giao tuyến a, và b. Do vậy, góc giữa 2 mặt phẳng P và Q chính là góc giữa a và b.

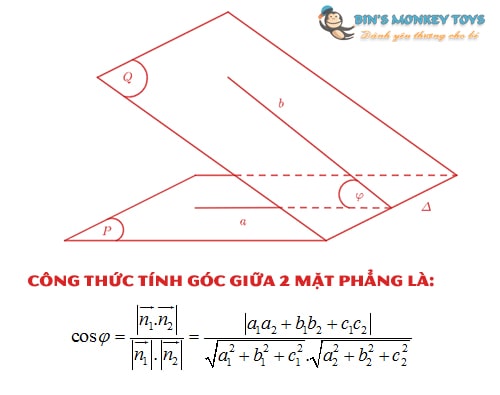
Công thức tính góc giữa 2 mặt phẳng trong không gian

Trong không gian Oxyz góc giữa 2 mặt phẳng được tính nhờ 2 vecto pháp tuyến tương ứng. Cụ thể, nếu 2 mặt phẳng P và Q có 2 phương trình là:

(P):  a₁x + b₁y + c₁z + d₁ = 0

(Q): a₂x + b₂y + c₂z + d₂ = 0

Từ đó ta có công thức tính góc giữa 2 mặt phẳng là:

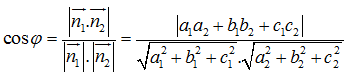
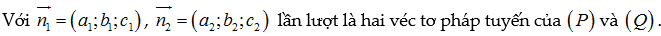
Bài tập tính góc giữa 2 mặt phẳng có lời giải chi tiết

Bài tập 1: Cho tứ diện đều MNPQ. Góc giữa MNP và MNQ bằng α. Tính góc giữa 2 mặt phẳng MNP và MNQ?

Lời giải

Đặt MN = a, Gọi I là trung điểm của MN

∆MNP đều cạnh a nên PI ⊥ MN và PI = a√3/2

∆MNP đều nên QI ⊥ MN và QI = a√3/2

• ((MNP), (MNQ)) = (PI, QI) = ∠PIQ = a

∆PIQ có:

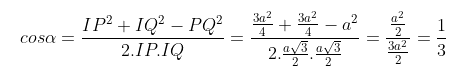
Đáp án: cosα = 1/3

Bài tập 2: Cho hình chóp tứ giác đều S.MNPQ có tất cả các cạnh đều bằng a. Hãy tính góc giữa một mặt bên và một mặt đáy?

Lời giải

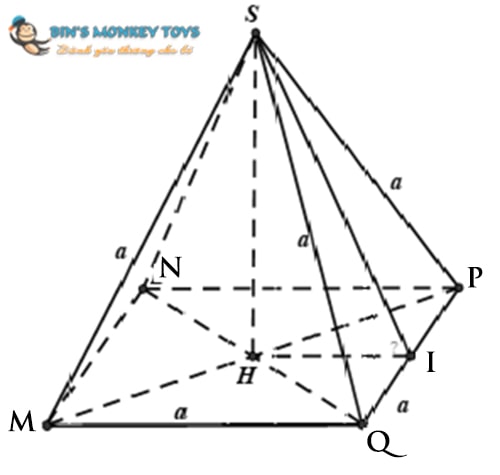
Gọi H là giao điểm của MP và NQ

Do S.MNPQ là hình chóp tứ giác đều nên SH ⊥ (MNPQ)

Ta có: (SPQ) ∩ (MNPQ) = PQ.

Gọi I là trung điểm của PQ

Tam giác SPQ là cân tại S.

∆PHQ cân tại H (Theo tính chất đường chéo hình vuông)

SI ⊥ PQ và HI ⊥ PQ

• ((SPQ), (MNPQ)) = (SI, HI) = ∠SIH = a

Tù đó ∆SPQ là tam giác đều cạnh a, có SM là đường trung tuyến

SM = a√3/2

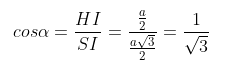
Hy vọng với kiến thức ở trên sẽ giúp các bạn nhớ công thức và từ đó dễ dàng áp dụng giải bài tập nhanh chóng. Bài tập tính góc giữa 2 mặt phẳng sẽ thật sự dễ dàng đối với những bạn học sinh nhớ công thức và chăm chỉ làm nhiều bài tập khác nhau.