Li độ là gì? Công thức tính li độ và bài tập có lời giải chi tiết

Bạn đang tò mò về li độ là gì? Công thức tính li độ? Một số bài tập thường gặp về li độ? Đừng lo, hãy cùng Góc Yêu Bé tìm hiểu chi tiết về vấn đề này qua bài viết dưới đây nhé.

Xem thêm:

• Công thức tính gia tốc góc và bài tập có lời giải
• Ý nghĩa về Omega? Công thức tính Omega?
• Công thức tính biên độ nhiệt và bài tập có lời giải
• Tổng hợp công thức tính xác suất thống kê và bài tập

Khái niệm về li độ

Li độ hay còn có tên gọi khác là độ dời chính là khoảng cách ngắn nhất từ một vị trí ban đầu đến vị trí hiện tại của một vật chuyển động. Nó thường được biểu diễn tọa độ của vật trong hệ quy chiếu khảo sát chuyển động.

Biểu đồ đô thị của li độ

Li độ trong dao động điều hòa chính là hàm cos và đô thị chính là hình sin

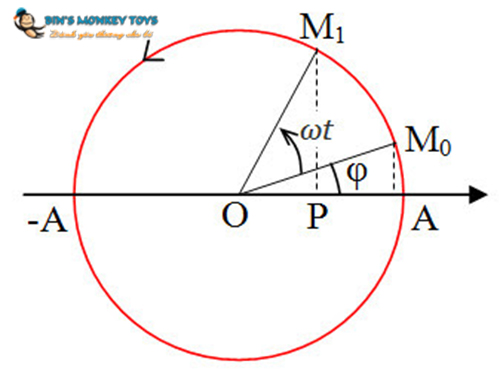
Công thức tính li độ

Công thức tính li độ là:

X = Acos (ωt + φ)

Trong đó x là li độ (có thể là âm hay dương)

                A là biên độ (cm, hay m) (không âm)

                ω là tần số góc (rad/s)

                 t là thời gian (s)

                 φ là pha ban đầu (rad)

                 (ωt + φ) là pha dao động tại thời điểm  

Bài tập tính li độ có lời giải chi tiết

Bài tập 1: Một vật dao động điều hòa với phương trình x = 3cos(3πt + π/3) (cm). Biết rằng ở thời điểm t có li độ là 2cm. Li độ dao động ở thời điểm sau đó 1/10 (s) bằng bao nhiêu?

Lời giải

Ở thời điểm t là:

X = 3cos(3πt + π/3) = 2cm

=) Cos(3πt + π/3) = 1

=) Sin(3πt + π/3)= 4/3

Tại thời điểm (t + 1/10) là

X = 3cos[3π(t + 1/10) + π/3]

    = 3cos(3πt + π/3 + π/2)

    = -3sin(3πt + π/3) = 2cm

Bài tập 2: Vật dao động điều hòa với biên độ A. Thời gian ngắn nhất vật đi từ vị trí có li độ A/2 đến vị trí có li độ A là 0,4s. Hỏi chu kỳ dao động của vật bằng bao nhiêu?

Lời giải

Dựa vào trục phân bố thời gian ta có thể tính được thời gian ngắn nhất đi từ x = A/2 đến x = A là T/6.

Do vậy T/6 = 0,4

=) T = 2,4 (s)

Bài tập 3: Một chất điểm dao động điều hòa với biên độ là 20cm và tần số góc là 20 rad/s. Khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ +5,5 cm đến vị trí cân bằng là bao nhiêu?

Lời giải

Thời gian ngắn nhất dao động điều hòa đi từ x = 5,5cm đến x = 0 bằng với thời gian chuyển động tròn đều đi từ M đến N là:

T = ∆φ/ω mà sin ∆φ = 5,5/20

=) ∆φ ≈ 0,275 (rad)

Nên t = ∆φ/ω = 0,275/20 ≈ 0,014 (s)

Trên đây là những thông tin về li độ, công thức tính li độ và một số bài tập thường gặp về li độ mà Góc Yêu Bé xin được gửi đến quý bạn đọc. Hy vọng thông qua bài viết này, các bạn sẽ củng cố được kiến thức, có thêm sự tự tin khi giải những bài tập về li độ.